Real-World Applications of Calculus
Calculus is a branch of mathematics that studies continuous change, and it plays a crucial role in a variety of fields, from science and engineering to economics and medicine. Understanding the principles of calculus allows professionals to model real-world scenarios and solve complex problems efficiently. This article will explore the diverse applications of calculus and how it helps us understand and shape the world around us.
Engineering Applications
In engineering, calculus is essential for designing and analyzing structures and systems. Engineers use calculus to determine how forces are distributed across structures, ensuring they can withstand various loads without failing. For example, in civil engineering, calculus helps calculate the stress and strain on materials when subjected to forces, allowing for safer and more efficient designs.
An engineering diagram showing forces acting on a structure.

Moreover, calculus is utilized in optimization problems, where engineers seek to maximize efficiency or minimize costs. For instance, when designing a bridge, calculus can help determine the most efficient shape that uses the least amount of material while maintaining structural integrity. By applying calculus principles, engineers can create innovative solutions that meet stringent safety standards while reducing costs.
For more insights on effective engineering practices, visit EssaySharp.com and check out this article on How Calculus is Used in Engineering.
Physics Applications
Calculus is fundamental in physics, particularly in understanding motion and the forces that affect it. Concepts such as velocity and acceleration are defined using derivatives, allowing physicists to describe how objects move over time. For example, when studying projectile motion, calculus can help determine the path of an object thrown into the air, factoring in gravity and air resistance.
Image Suggestion: A graph illustrating projectile motion.
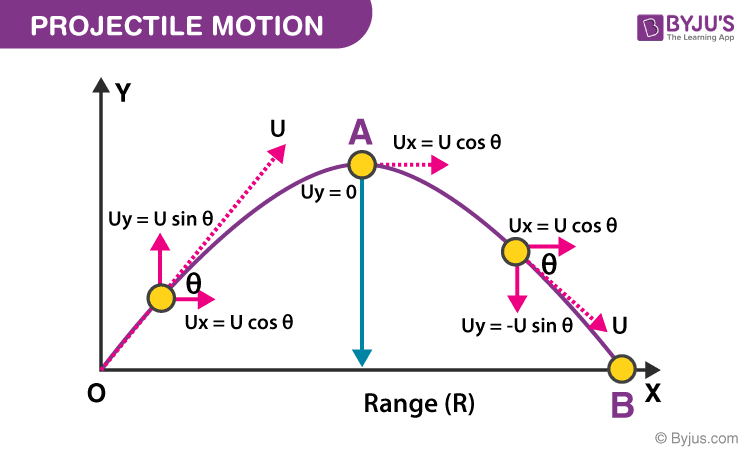
In addition, calculus is vital in understanding electrical circuits. Engineers use calculus to model how current and voltage change over time in capacitors and inductors, which is crucial for designing effective electrical systems. Fluid dynamics, the study of how liquids and gases move, also relies heavily on calculus, as it helps predict how fluids flow under various conditions.
To learn more about how calculus is used in physics, check out EssaySharp and read this article on Calculus in Physics.
Economics and Business Applications
In economics, calculus is a powerful tool for analyzing and optimizing financial outcomes. Businesses use calculus to model supply and demand, allowing them to determine the optimal price for their products. By analyzing the marginal cost—an important concept derived from calculus—companies can make informed decisions about production levels to maximize profits.
Image Suggestion: A graph showing supply and demand curves.
For instance, if a company wants to know how changes in production affect costs, it can apply calculus to understand the relationship between these variables. By calculating the cost function derivative, businesses can identify the most cost-effective strategies to increase production without incurring excessive expenses.
Explore more about economics and business strategies on EssaySharp and check out this resource on Calculus in Economics.
Biology and Medicine Applications
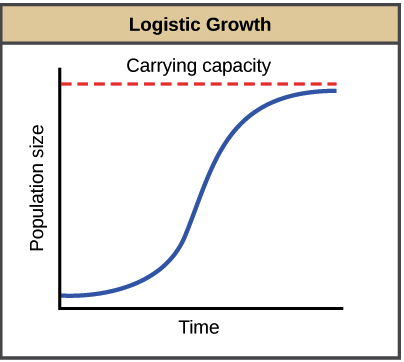
Calculus is also used extensively in biology and medicine. One significant application is in modeling population dynamics, where differential equations help predict how populations of species change over time due to factors like birth rates, death rates, and migration. These models are crucial for conservation efforts and understanding ecosystem dynamics.
Image Suggestion: A graph showing population growth models.
In the medical field, calculus aids in determining drug dosage levels that ensure efficacy while minimizing side effects. By using calculus to model how drugs disperse in the body, healthcare professionals can devise optimal treatment plans tailored to individual patients.
Conclusion
The applications of calculus in the real world are vast and varied, impacting many aspects of our daily lives. From engineering and physics to economics and biology, calculus provides the tools needed to understand and address complex challenges. As we continue to face new problems, the role of calculus in developing innovative solutions will only become more significant. By appreciating the value of calculus, we can better understand the world around us and the mathematics that underpin it.
If you need assistance with calculus or handling complex assignments, I’m here to help! At EssaySharp, I assist students in tackling challenging coursework and ensuring they succeed in their studies.
